Shooting Tips
Making Sense of Steep Angle Shots
Based on the works of Tom Henderson, Steve Mansour, Perry Ratcliff, and Thomas L. Liston. Edited by Steve Russell
Quick Explanation
The most common rule about uphill/downhill shots is that you shoot for the horizontal component of the range to the target.
For example, if you were shooting a 40 yard uphill shot at a 30 degree angle you would set your sights for about 35 yards (the cosine of the 30 degree angle times the line-of-sight distance to the target - which in this instance comes out to 0.866 times 40 yards = 34.6 yards). This would represent the actual horizontal range to the target and is a pretty good starting point.
For distances from about 20 to 40 yards this works pretty well depending on a variety of factors such as bow speed and arrow size, weight, and drag.
For shorter distances, less than about 20 yards, you run in to increasing parallax errors with either sights or your basic eyeball. For distances longer than about 40 yards you begin to feel more of the effects of drag.
You can take the above and apply it in practice to see how well it works for you.
As stated, it is dependent on several factors so your mileage may vary. Of course, you're going to say, "How can I tell at what angle the shot is?", and the reply has to be get a protractor, electronic level, or simply measure the horizontal and vertical components to a known distance angle shot and try it out.
This is the simple explanation.
However, if you're into it we invite you to follow along on a more involved discussion of the problem.
Of the two major factors affecting arrow flight - drag and gravity - certainly the easiest to work with is gravity.
We'll reserve the discussion on drag for another time and focus on the effects of gravity starting with the concept of a free-falling object.
Free Fall
A free-falling object is one whose downward acceleration is caused by the force of gravity alone. Earth exerts an acceleration of about -10m/s/s (actually -9.8 meters per second per second or -9.8m/s2). An object held at rest and then released will accelerate downwards at about -10m/s2 for every second it is falling. An object thrown or shot from cannon or bow will accelerate downwards at the same rate - it will just go horizontally while it is also accelerating downwards at -10m/s2.
Since this site deals with ranges in feet (and yards) we'll use the actual acceleration of -9.8m/s2 and convert it to feet so that the effect of gravity will be represented as an acceleration of -32 f/s2 (well, actually -32.152 feet/second2 but we'll round things off for convenience).
The Effect Of Gravity
With the Earth exerting a pull of -32 f/s2 that means that an object starting at a stationary location and then released in free fall will accelerate to and be traveling at -32 f/s after the first second, -64 f/s after the second, -96 f/s after the third, and so on. It doesn't matter if the object has a horizontal velocity or not: it still falls, or accelerates, at -32 f/s2.
When shot from a bow an arrow is accelerated to its maximum speed and then continues on it's own inertia. Without the effects of drag or gravity it would continue along it's initial path forever or until it hits something. However, just as in our stationary object above, our arrow feels the same gravitational effect and falls at the same rate of -32 feet/second2.
Projectile Model
At launch our arrow becomes a simple projectile - we accelerate it to a constant speed, launch it at a given angle, and then it travels in a parabolic path to the target. The only force acting on our arrow in flight (ignoring drag) is the acceleration of gravity which we know to be a constant -32 feet/second2.
Using kinematic equations (learned and forgotten in high school) we can solve simple projectile motion problems involving arrow flight. (Kids - stay in school: you will use that information at some time in your life!)
Calculating Arrow Path - Level Shot
The effect of gravity is only felt after some duration of time. We'll need to work with a shot model that lets gravity have a chance to modify our flight profile measurably so lets look at a horizontal shot of 40 yards.
We know the distance involved and the acceleration of gravity. The last element needed is the speed of the arrow.
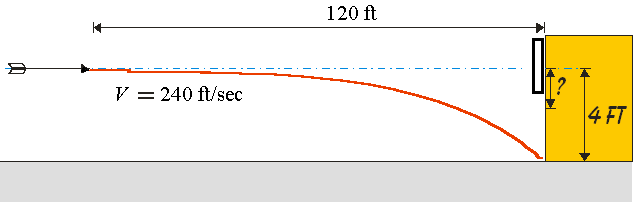
Our test case will be as follows: An arrow is shot parallel to the ground at a target 40 yards away. Starting at a shooting height of four feet above the ground our bow gives the arrow an initial velocity of 240 feet per second (240 fps). The initial course is shown as the blue dashed line leading towards the target spot four feet above the ground. Gravity will begin pulling it off this course the instant it leaves the bowstring and is represented by the red line shown below.
The question is; how much will gravity pull the arrow down before it strikes the target?
